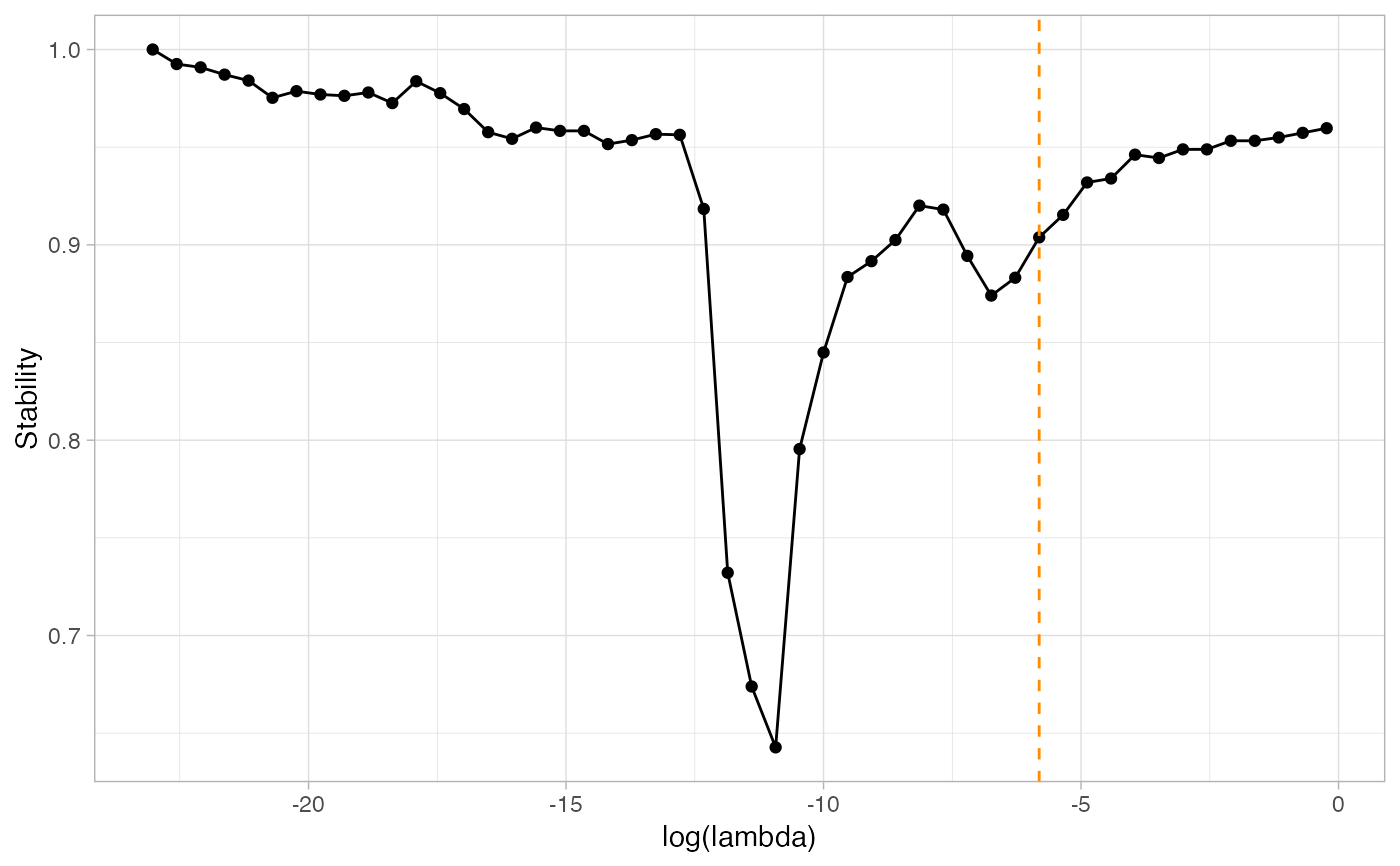
Stability Approach to Threshold Selection

Source: R/F_inference.R

Stability Approach to Threshold Selection

StATS(Pmat, nlambda = 100, stab.thresh = 0.9, plot = FALSE)

Arguments

Pmat

Pmat output from the `ResampleEMtree()` function
nlambda

Number of probability thresholds to look at
stab.thresh

Stability threshold
plot

Optional graphic output

Value

a list containing

  • freqs_opt: A tibble with (number of possible edges) x nlambda rows, containing the computed selection frequency of each edge and stability measure for each threshold.

  • lambda_opt: The probability threshold giving the desired stability of frequencies.

  • plot: The optional graphic output.

Examples

n=100
p=15
S=15
set.seed(2021)
simu=data_from_scratch("erdos",p=p,n=n)
G=1*(simu$omega!=0) ; diag(G) = 0
#With default evaluation, using the PLNmodel paradigm:
default_resample=ResampleEMtree(simu$data, S=S, cores = 1)

#> Computing 15 probability matrices with 1 core(s)... 
#> Convergence took 0.27 secs  and  30  iterations.
#> Convergence took 0.27 secs  and  20  iterations.
#> Convergence took 0.3 secs  and  30  iterations.
#> Convergence took 0.36 secs  and  30  iterations.
#> Convergence took 0.24 secs  and  19  iterations.
#> Convergence took 0.33 secs  and  30  iterations.
#> Convergence took 0.27 secs  and  30  iterations.
#> Convergence took 0.46 secs  and  30  iterations.
#> Convergence took 0.31 secs  and  30  iterations.
#> Convergence took 0.28 secs  and  30  iterations.
#> Convergence took 0.23 secs  and  16  iterations.
#> Convergence took 0.24 secs  and  30  iterations.
#> Convergence took 0.32 secs  and  30  iterations.
#> Convergence took 0.24 secs  and  23  iterations.
#> Convergence took 0.24 secs  and  23  iterations.4.48 secs 
stab_selection=StATS(default_resample$Pmat, nlambda=50, stab.thresh=0.9,plot=TRUE)

#Check quality of result
table(pred=1*(stab_selection$freqs_opt>0.9), truth=ToVec(G))

#>     truth
#> pred  0  1
#>    0 91  1
#>    1  0 13